Circuito abierto
Un circuito abierto es un circuito eléctrico en el cual no circula la corriente eléctrica por estar éste interrumpido o no comunicado por medio de un conductor eléctrico. El circuito al no estar cerrado no puede tener un flujo de energía que permita a una carga, o a un receptor de energía, aprovechar el paso de la corriente eléctrica y poder cumplir un determinado trabajo.
CONCEPTO DE CIRCUITO ABIERTO
Un circuito abierto es un circuito en el que la fuente de energía existente no produce una fuerza suficiente para vencer la resistencia del circuito, por lo que no fluye corriente a través de el. Este efecto se produce a causa de una resistencia muy grande ya sea una interrupción en el circuito para lo que se diría que la resistencia es el aire, o una resistencia con un valor capaz de aislar la corriente en el circuito.
I=V/R
I=9v/R®¥
I®0
Al ser la resistencia tan grande la corriente es cero o nula ya que no es posible establecer un flujo de electrones.
Un circuito abierto es un circuito en el que la fuente de energía existente no produce una fuerza suficiente para vencer la resistencia del circuito, por lo que no fluye corriente a través de el. Este efecto se produce a causa de una resistencia muy grande ya sea una interrupción en el circuito para lo que se diría que la resistencia es el aire, o una resistencia con un valor capaz de aislar la corriente en el circuito.
I=V/R
I=9v/R®¥
I®0
Al ser la resistencia tan grande la corriente es cero o nula ya que no es posible establecer un flujo de electrones.
Circuito RC
Un circuito RC es un circuito compuesto de resistencias y condensadores alimentados por una fuente eléctrica. Un circuito RC de primer orden está compuesto de un resistor y un condensador y es la forma más simple de un circuito RC. Los circuitos RC pueden usarse para filtrar una señal, al bloquear ciertas frecuencias y dejar pasar otras. Los filtros RC más comunes son el filtro paso alto, filtro paso bajo, filtro paso banda, y el filtro elimina banda. Entre las características de los circuitos RC está la propiedad de ser sistemas lineales e invariantes en el tiempo; reciben el nombre de filtros debido a que son capaces de filtrar señales eléctricas de acuerdo a su frecuencia.
En la configuración de paso bajo la señal de salida del circuito se coge en bornes del condensador, estando este conectado en serie con la resistencia. En cambio en la configuración de paso alto la tensión de salida es la caída de tensión en la resistencia.
Este mismo circuito tiene además una utilidad de regulación de tensión, y en tal caso se encuentran configuraciones en paralelo de ambos, la resistencia y el condensador, o alternativamente, como limitador de subidas y bajas bruscas de tensión con una configuración de ambos componentes en serie. Un ejemplo de esto es el circuito Snubber.
Los circuitos RC son circuitos que están compuestos por una resistencia y un condensador.
Se caracteriza por que la corriente puede variar con el tiempo. Cuando el tiempo es igual a cero, el condensador está descargado, en el momento que empieza a correr el tiempo, el condensador comienza a cargarse ya que hay una corriente en el circuito. Debido al espacio entre las placas del condensador, en el circuito no circula corriente, es por eso que se utiliza una resistencia.
ARGA DE UN CONDENSADOR
Ya se conoce que las variables dependiendo del tiempo serán I y q. Y la corriente I se sustituye por dq/dt (variación de la carga dependiendo de la variación del tiempo):
(dq/dt)R = V – (q/C)
dq/dt = V/R – (q/(RC))
Esta es una ecuación
Diferencial. Se pueden dq/dt = (VC – q)/(RC)
Separar variable dq/(q – VC) = - dt/(RC)
Al integrar se tiene ln [ - (q – VC)/VC)] = -t/(RC
Despejando q q dt = C V [(1 – e-t/RC )] = q (1- e-t/RC )
El voltaje será
DESCARGA DE UN CONDENSADOR
Debido a que la diferencia de potencial en el condensador es IR = q/C, la razón de cambio de carga en el condensador determinará la corriente en el circuito, por lo tanto, la ecuación que resulte de la relación entre el cambio de la cantidad de carga dependiendo del cambio en el tiempo y la corriente en el circuito, estará dada remplazando I = dq/dt en la ecuación de diferencia de potencial en el condensador:
q = Q e-t/RC
Donde Q es la carga máxima
La corriente en función del tiempo entonces, resultará al derivar esta ecuación respecto al tiempo:
I = Q/(RC) e-t/RC
Se puede concluir entonces, que la corriente y la carga decaen de forma exponencial.
Circuito RL
Un circuito RL es un circuito eléctrico que contiene una resistencia y una bobina en serie. Se dice que la bobina se opone transitoriamente al establecimiento de una corriente en el circuito.
La ecuación diferencial que rige el circuito es la siguiente:
Donde:
Régimen transitorio[editar]
La solución general, asociada a la condición inicial
 , es: , es:
Dónde:
La constante de tiempo
 caracteriza la « duración » del régimen transitorio. Así, la corriente permanente del circuito se establece a 99% después de una duración de 5 caracteriza la « duración » del régimen transitorio. Así, la corriente permanente del circuito se establece a 99% después de una duración de 5  . .
Cuando la corriente se convierte en permanente, la ecuación se simplifica en
 , ya que , ya que 
Circuito RLC en serie[editar]Circuito sometido a un escalón de tensión[editar]
Si un circuito RLC en serie es sometido a un escalón de tensión
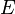 , la ley de las mallas impone la relación: , la ley de las mallas impone la relación:
Introduciendo la relación característica de un condensador:
Se obtiene la ecuación diferencial de segundo orden:
Donde:
En el caso de un régimen sin pérdidas, esto es para
 , se obtiene una solución de la forma: , se obtiene una solución de la forma:
Donde:
Lo que resulta:
Donde
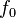 es la frecuencia de resonancia, en hercios (Hz). es la frecuencia de resonancia, en hercios (Hz).Circuitos sometidos a una tensión sinusoidal[editar]
La transformación compleja aplicada a las diferentes tensiones permite escribir la ley de las mallas bajo la forma siguiente:
siendo, introduciendo las impedancias complejas:
La frecuencia angular de resonancia en intensidad de este circuito ω0 es dada por:
Para esta frecuencia la relación de arriba se convierte en:
Circuito RLC en paralelo[editar] 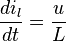 
ya que
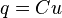  
Atención, la rama C es un corto-circuito:de esta manera no se pueden unir las ramas A y B directamente a los bornes de un generador E, se les debe adjuntar una resistencia.
Las dos condiciones iniciales son:
Circuito sometido a una tensión sinusoidal[editar]
La transformación compleja aplicada a las diferentes intensidades proporciona:
Siendo, introduciendo las impedancias complejas:
La frecuencia angular de resonancia en intensidad de este circuito ω0 es dada por:
Para esta frecuencia la relación de arriba se convierte en:
|




 es la
es la  es la
es la  es la
es la 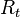 es la
es la 

 es la intensidad de la
es la intensidad de la  es el
es el 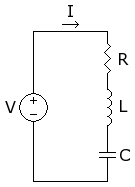







![\underline {U_G} = - \frac{j}{C \omega} \underline I + j L \omega \underline I + R_{t} \underline I = \bigg[ R_t + j \frac{LC \omega^2 - 1}{C \omega} \bigg] \underline I](https://upload.wikimedia.org/math/a/3/2/a3299971c511a4b8b5c8957f837aca51.png)
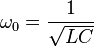



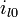 conserva su valor antes de la puesta en tensión (porque la inductancia se opone a la variación de corriente).
conserva su valor antes de la puesta en tensión (porque la inductancia se opone a la variación de corriente). conserva su valor antes de la puesta en tensión
conserva su valor antes de la puesta en tensión  .
.

![\underline I = \left[ \frac{1}{R} + j (C \omega - \frac{1}{L \omega}) \right] \underline U](https://upload.wikimedia.org/math/8/6/4/8640a8358611b48e02390533687a5b8d.png)


No hay comentarios:
Publicar un comentario